A modus ponens az egyik legalapvetőbb következtetési szabály. Ha valakinek el kell magyarázni, hogy fest egy érvényes deduktív következtetés, rendszerint ezt hozzuk példának, s ilyesmiket mondunk:
Ha esik az eső, (akkor) nedves a járda. Esik az eső \ Nedves a járda.
Ha Othello féltékeny, (akkor) megfojtja Desdemonát. Othello féltékeny. \ Othello megfojtja Desdemonát.
Ha szeret, (akkor) meg fogod neked bocsátani. Szeret. \ Meg fog neked bocsátani.
Ezeket az teszi a modus ponens eseteivé, hogy az alábbi sémára épülnek:
(MP) Ha 1, akkor 2. 1. \ 2.
Ezt a következtetést még akkor is érvényesnek találjuk, ha a számozott helyekre értelmetlen mondatokat írunk.
Ha miffen, akkor muffog. Miffen. \ Muffog.
Jelentsen bármit a miffenés és a muffogás, ha a premisszák igazak, a konklúzió nem lehet hamis – pontosan az ilyen következtetést nevezzük deduktíve érvényesnek.
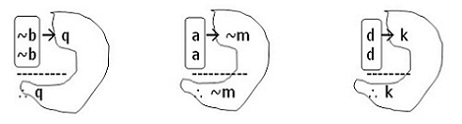
A helyzet azonban, úgy tűnik, nem ilyen egyszerű. „Ha akkor”-ból ugyanis kettő is van. Van először is a logikusok háziasított „ha, akkor”-ja, melyet materiális kondicionálisnak neveznek. Ez szelíd: megengedi, hogy néhány egyszerű szabállyal jellemezzük, és olyan jól van idomítva, hogy még csak eszébe sem jut megsérteni a modus ponenst. Csakhogy ez nem azonos a „ha, akkor” vadon élő változatával, azzal, amely ténylegesen része a természetes nyelvnek. (Például: a materiális kondicionálissal képzett mondat automatikusan igaz, ha a „ha” utáni tagmondat hamis. A „ha, akkor” szokásos értelmezése mellett azonban azt a mondatot, hogy „Ha levágják a fejem, feltámadok”, nem teszi automatikusan igazzá, az, hogy nem vágják le a fejem.)
Bennünket most éppen ez a vadon élő változat, az indikatív kondicionális érdekel. Ez pedig olykor zavarba ejtő eseteket produkál. Mielőtt erre rátérnénk, látnunk kell, hogy a modus ponenst nem érdekli, hogy benne mennyire összetett mondatok szerepelnek. Lehet az 1-es helyre írt mondat egy kilométer hosszú, a 2-es helyre írt két kilométer hosszú. És akkor jöjjenek a példák. Mindkettő némi magyarázatot igényel.
1980-ban vagyunk nem sokkal az amerikai elnökválasztás előtt. A közvélemény-kutatások szerint Ronald Reagan, a republikánus jelölt, biztosan vezet. A második helyen a demokrata jelölt áll, Gerald Ford. Messze leszakadva tőlük, de még versenyben van egy másik republikánus is, John Anderson. Ebben a helyzetben igaznak tartjuk a következőket.
Egy republikánus nyer. (Hiszen Reagan vezet.)
Ha egy republikánus nyer, akkor, ha nem Reagan nyer, akkor Anderson nyer. (Rajtuk kívül nincs más republikánus jelölt.)
Ezekből viszont modus ponensszel az következik, hogy
Ha nem Reagan nyer, akkor Anderson nyer.
De ez hamis. Ha Reagan veszít, Ford lesz a befutó, nem pedig a teljesen lemaradt Anderson.
A másik példa. A tüdőshalakról tudni kell, hogy a szárazföldön élnek, és egyáltalán nem fordulnak elő a tengerben, kivéve, ha a példagyártásban mesterkedő filozófusok oda nem hajítják őket. Szóval éppen a nyílt tengeren horgászol, amikor valami lerántja az úszót. Ekkor feltehetően igaznak tartanád az alábbiakat.
Ez a valami egy hal. (Ez a legsanszosabb, nem?)
Ha ez a valami egy hal, akkor, ha tüdeje van, akkor tüdőshal. (Hiszen minden hal, amelynek tüdeje van, tüdőshal.)
Modus ponensszel következik, hogy:
Ha ennek a valaminek tüdeje van, akkor tüdőshal.
De ezt nem tarthatod igaznak, mert a tengerben nincsenek tüdőshalak. Ha annak, amit fogtál, tüdeje van, akkor szégyelld magad, mert egy delfint fogtál! (Vagy egy bálnát. Ekkor szégyenkezés helyett mentsd a bőröd.)
 Vannak tehát olyan következtetések, amelyek szabályos modus ponensek, azaz igazodnak (MP)-hez, csakhogy igaz premisszákról hamis konklúzióra vezetnek. Márpedig egy érvényes következtetés nem vezethet igaz premisszákról hamis konklúzióra. Úristen! Lehet, hogy a modus ponens, amelyet imádunk, s amellyel serdülő gyermekeinket logikára tanítjuk, az indikatív kondicionálissal nem érvényes? Vagy inkább az ilyen példákkal van baj?
Vannak tehát olyan következtetések, amelyek szabályos modus ponensek, azaz igazodnak (MP)-hez, csakhogy igaz premisszákról hamis konklúzióra vezetnek. Márpedig egy érvényes következtetés nem vezethet igaz premisszákról hamis konklúzióra. Úristen! Lehet, hogy a modus ponens, amelyet imádunk, s amellyel serdülő gyermekeinket logikára tanítjuk, az indikatív kondicionálissal nem érvényes? Vagy inkább az ilyen példákkal van baj?
Na, mit gondolsz?
Vann McGee nyomán






 A törpedobás hanyatlása az évtized végén kezdődött, amikor a Little People of Americának, a törpék jogvédő szervezetének nyomására a floridai törvényhozás betiltotta törpedobást, 1000 dolláros bírsággal és az alkoholárusítási engedély visszavonásával fenyegetve a törpedobásnak helyt adó létesítményeket. Ezt világszerte hasonló tilalmak követték. A franciaországi Morsang-sur-Orge városkában elrendelt tilalomról még az ENSZ Emberi Jogok Bizottsága (2006 óta Emberi Jogi Tanács) is állást foglalt, s kimondta, hogy a tilalom fenntartható, mert a törpedobás súlyosan sérti a törpék emberi méltóságát.
A törpedobás hanyatlása az évtized végén kezdődött, amikor a Little People of Americának, a törpék jogvédő szervezetének nyomására a floridai törvényhozás betiltotta törpedobást, 1000 dolláros bírsággal és az alkoholárusítási engedély visszavonásával fenyegetve a törpedobásnak helyt adó létesítményeket. Ezt világszerte hasonló tilalmak követték. A franciaországi Morsang-sur-Orge városkában elrendelt tilalomról még az ENSZ Emberi Jogok Bizottsága (2006 óta Emberi Jogi Tanács) is állást foglalt, s kimondta, hogy a tilalom fenntartható, mert a törpedobás súlyosan sérti a törpék emberi méltóságát. Ugyanez
Ugyanez